Статистика: Распределение суммы экспоненциально распределенных случайных величин
Сотрудник следит за тем, чтобы сервер работал исправно. В сервере установлена плата стандартного образца. Как только он замечает поломку, он мгновенно меняет плату на новую плату усиленного образца. Когда ломается и эта плата, сервер перестаёт работать. Плата стандартного образца ломается в среднем раз в 10 месяцев. Плата усиленного образца ломается в среднем раз в 20 месяцев. Найдите вероятность, что сервер проработает менее 2 лет.
Решение.
Обозначим время работы платы стандартного образца за Х, а время службы платы усиленного образца за Y. Обе величины распределены экспоненциально. Время работы сервера, которое мы обозначим за Z, равно сумме времени работы обеих плат, т.е. Z=X+Y. Фактически, задача сводится к тому, чтобы найти вероятность, что X+Y будет меньше 24.
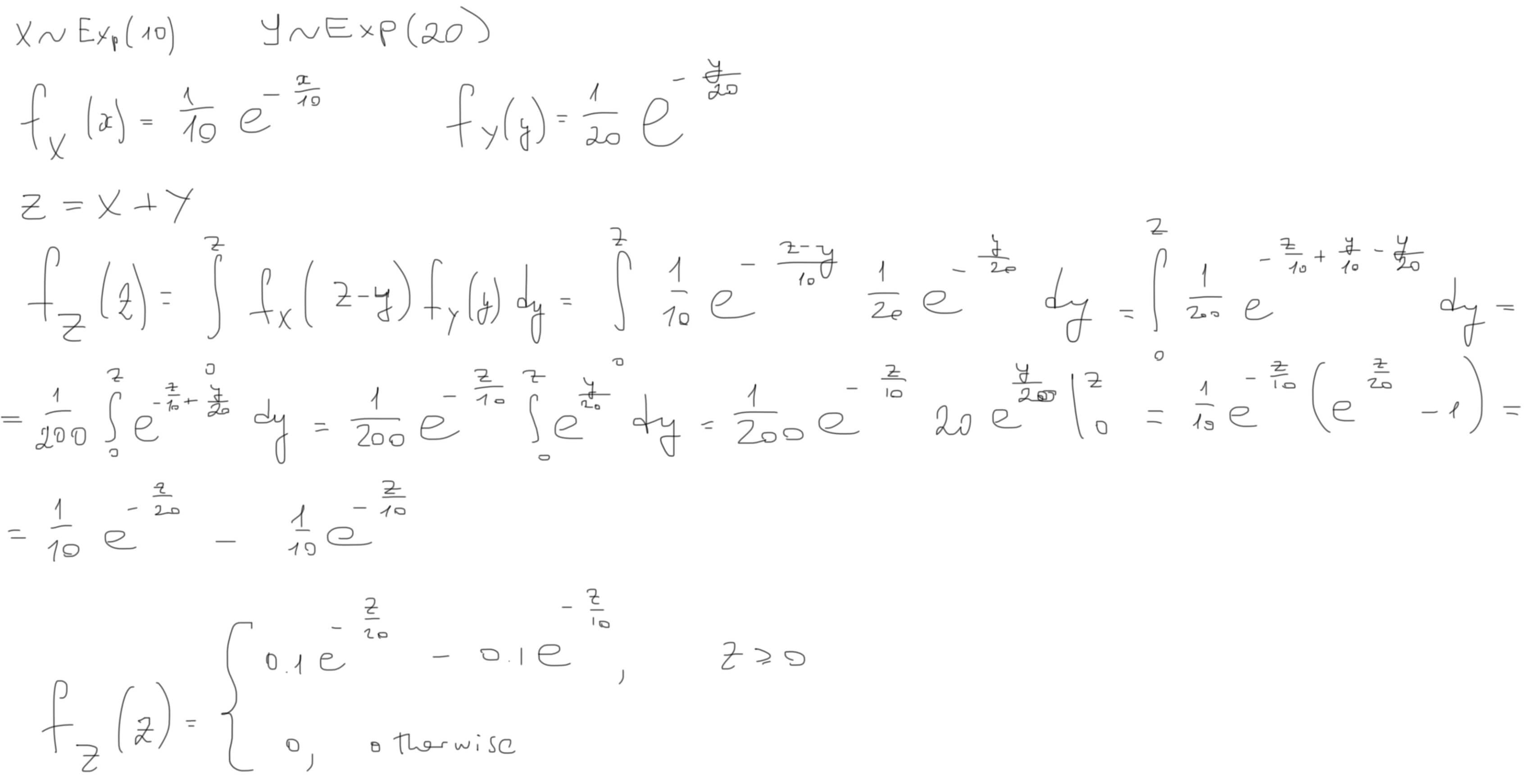
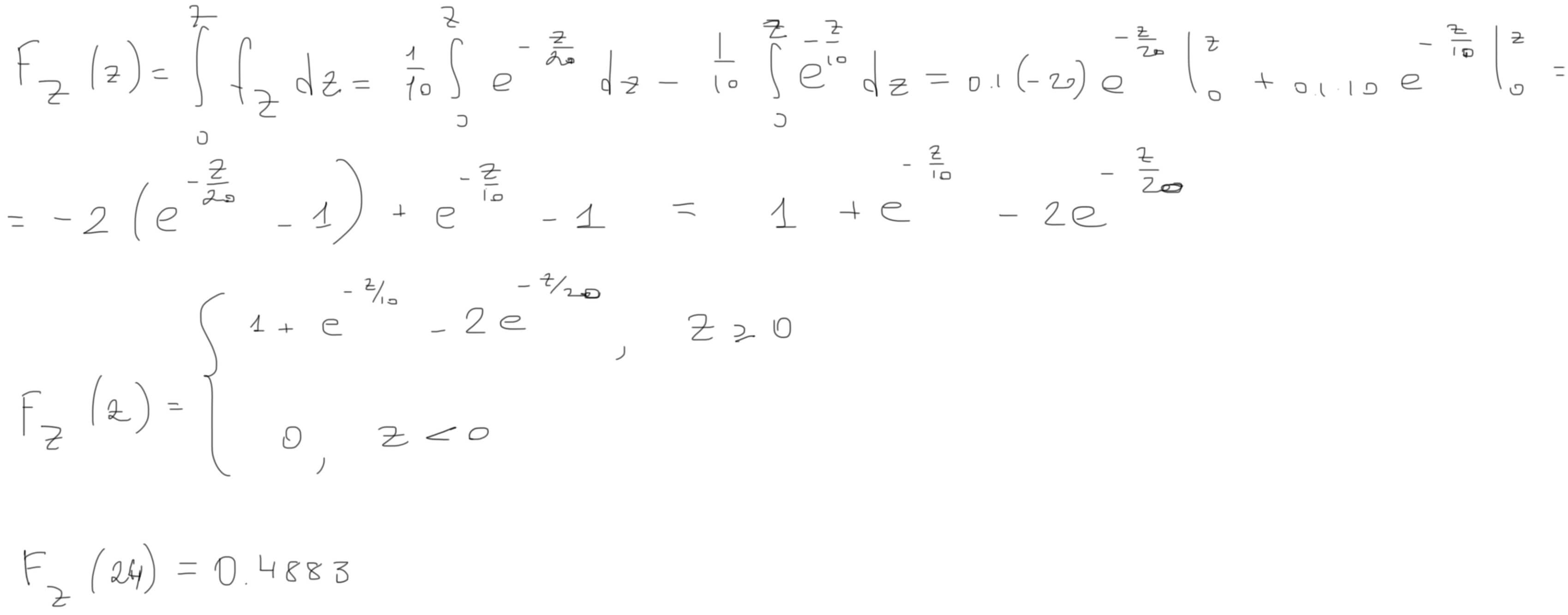
Вероятность равна 48.83%.
12.10.2020